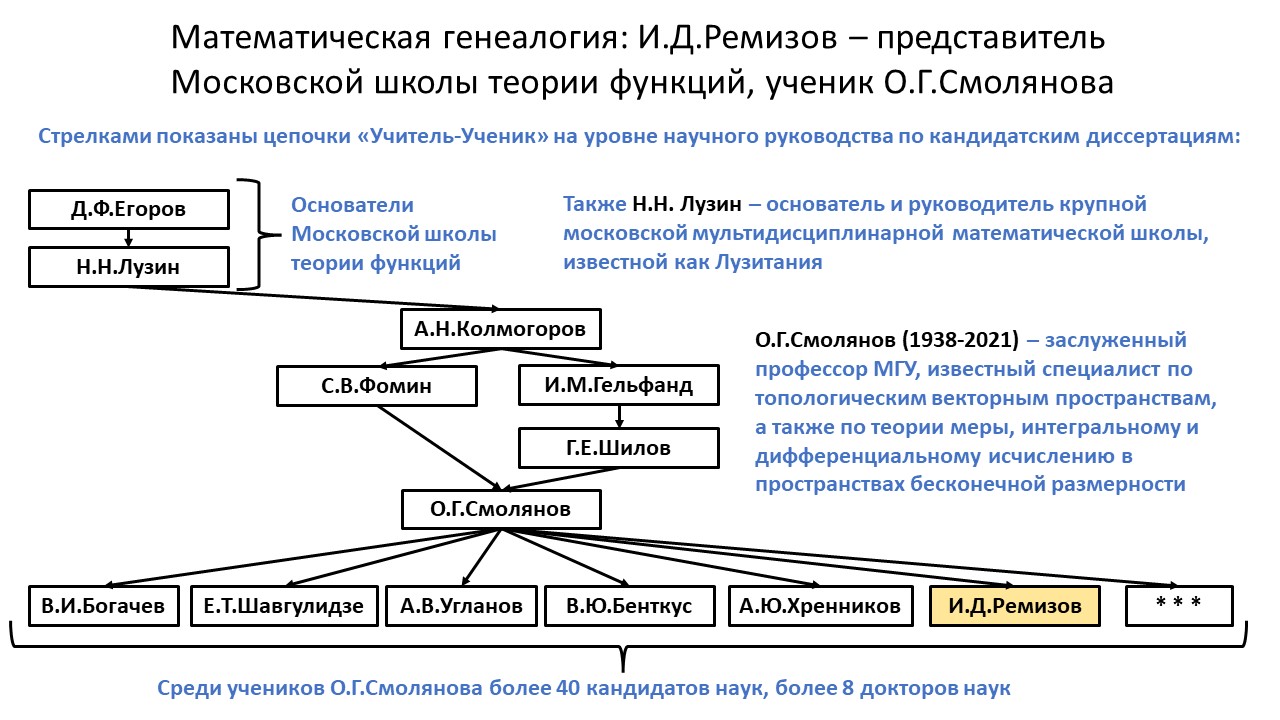
Научная работа посвящена созданию и исследованию новых конструкций, основанных на идеях и методах функционального анализа. Эти конструкции применяются затем для решения задач теории дифференциальных уравнений и вычислительной математики.

Тематика исследований в основном относится к построению и исследованию основанных на теореме Чернова методов аппроксимации сильно непрерывных полугрупп линейных ограниченных операторов в банаховом пространстве (также называемых $С_0$-полугруппами). Эти методы позволяют выражать сколь угодно точные аппроксимации к решениям линейных дифференциальных уравнений в явном виде через коэффициенты этих уравнений - произвольные функции, играющие роль параметров. Эта ситуация аналогична выражению корней квадратного трёхчлена через его коэффиценты в элементарной математике. Построенные И.Д.Ремизовым методы применимы к обыкновенным дифференциальным уравнениям, а также к уравнениям в частных производных: параболическим, эллиптическим и уравнениям типа Шрёдингера. Аппроксимации к решению через коэффициенты уравнения выражаются с помощью формул Фейнмана, а также с помощью двух новых типов формул, впервые построенных в работах И.Д.Ремизова: квазифейнмановских интегральных формул и формул, полученных с помощью оператора сдвига. Эти аппроксимации носят конструктивный характер (имеется ясный алгоритм вычисления), в некоторых случаях доказаны оценки на скорость сходимости аппроксимаций к точному решению уравнения.

Полученные научные результаты (по состоянию на март 2023)

1. Совместно с А.В.Савватеевым найден субдифференциал функционала вычисления максимума на пространстве всех вещественных функций, непрерывных на метрическом компакте $K$. А именно, показано, что если $Mf=\max_{x\in K}f(x)$, то субдифференциал функционала $M$, вычисленный на функции $f$, совпадает с множеством всех вероятностных мер на аргмаксимуме $f$.

2. Для параболического уравнения с переменными коэффициентами с пространственной координатой из бесконечномерного гильбертова пространства доказано существование разрешающей полугруппы, найдена дающая решение задачи Коши формула Фейнмана, доказана непрерывная зависимость решения от коэффициентов уравнения. (Статьи: Russ.J.Math.Phys. 2012, Модел. и анализ информ. систем 2015, IDAQP 2018).

3. Для параболического уравнения на вещественной прямой с переменными коэффициентами построены основанные на операторах сдвига черновские аппроксимации к решению задачи Коши, доказана равномерная сходимость аппроксимаций к решению. Доказано, что решение может быть записано как формула Фейнмана с интегральным ядром, содержащим обобщённые функции. (Статьи: ДАН 2017, Appl.Math.Comp. 2018)

4. То же самое, что и в п.3, сделано в $\mathbb{R}^n$. (Статья: J.Math.Phys. 2019)

5. Введено понятие функции, касательной по Чернову к оператору, и найдены методы построения таких функций. (Cтатьи: ДАН 2017, Дифф. уравнения 2017)

6. Открыта формула $R(t)=\exp(ia(S(t)-I))$, позволяющая по самосопряжённой касательной Чернова $S$ к произвольному самосопряжённому оператору $H$ при помощи теоремы Чернова построить сильно непрерывную группу унитарных операторов $e^{iatH}$, где $a$ -- ненулевое вещественное число (например, 1 или -1). Эта формула позволяет строить представления решений широкого класса уравнений Шрёдингера, для полученных представлений И.Д.Ремизов ввёл термин "квазифейнмановские формулы" (Статьи: J.Funct.Anal. 2016, ДАН 2017)

7. В виде квазифейнмановских формул, построенных на основе интегрального оператора совместно с Д.В.Гришиным найдены решения одномерного уравнения Шредингера с гамильтонианом вида квадрат импульса плюс гладкий ограниченный потенциал (Статья: Вестник МГТУ 2017)

8. В виде квазифейнмановских формул, построенных на основе оператора сдвига найдены решения одномерного уравнения Шредингера с гамильтонианом вида квадрат импульса плюс локально квадратично интегрируемый потенциал (Статья: Матем. заметки 2016)

9. В виде квазифейнмановских формул найдены решения конечномерного уравнения Шредингера с гамильтонианом вида квадрат импульса плюс потенциал (Статьи: Матем. заметки 2018, Potential Anal. 2020)

10. В виде квазифейнмановских формул найдены решения одномерного уравнения Шредингера с гамильтонианом, содержащим производные сколь угодно высокого порядка, умноженные на переменные коэффициенты. (Статья: Potential Anal. 2020)

11. Построены примеры, показывающие, что сходимость в теореме Чернова может быть сколь угодно быстрой и сколь угодно медленной. (Статьи: Матем. заметки 2020, Матем. заметки 2022)

12. Совместно с О.Е.Галкиным доказаны оценки сверху на скорость сходимости черновских аппроксимаций в общем случае. Кратко результат формулируется так: чем больше производных в нуле совпадает у полугруппы и её функции Чернова, тем выше будет скорость сходимости черновских аппроксимаций к полугруппе. В типичном случае при совпадении первых $k$ производных невязка убывает как $const/n^k$ при $n\to\infty$, но при неудачно выбранной функции Чернова сходимость может быть гораздо медленнее. (Статьи: Матем. заметки 2020, Матем. заметки 2022 + статьи на рассмотрении в журналах).

13. Открыт метод построения быстро сходящихся черновских аппроксимаций, совместно с А.В.Ведениным построены примеры таких аппроксимаций. (Статья на рассмотрении в журнале)

14. Совместно с К.А.Драгуновой, А.А.Гаращенковой, Н.Никбахт исследована зависимость скорости сходимости черновских аппроксимаций в сильной операторной топологии от вектора, на котором рассматривается сходимость операторов. (Статья на рассмотрении в журнале)

15. Открыт метод построения черновских аппроксимаций для резольвент операторов, являющихся генераторами $C_0$-полугрупп. С помощью этого метода построены черновские аппроксимации к решениям обыкновенных дифференциальных уравнений с переменными коэффициентами. (Статья на рассмотрении в журнале, доступен препринт)

16. Совместно с С.Мадзуки, В.Моретти и О.Г.Смоляновым построены равномерно сходящиеся черновские аппроксимации к решениям параболического уравнения на некомпактном многообразии (Статья Math.Nacht. 2023)

Темы в работе (по состоянию на март 2023)

1. Исследование скорости сходимости черновских аппроксимаций (большое направление, много задач). 2. Построение черновских аппроксимаций к решениям эллиптических уравнений с частными производными. 4. Построение черновских аппроксимаций к решениям уравнений четвёртого порядка. 5. Исследование соприкасающихся клотоид и порождаемых ими кривых. 6. Исследования по психофизиологии эмоций.

Образование

Окончил физико-математический лицей №40 (г. Нижний Новгород) в 2002 году, поступил в Нижегородский государственный университет им. Н.И.Лобачевского на механико-математический факультет (где неформально был учеником доцента А.В.Абросимова). Лето 2004 года провёл в Израиле, на позиции visiting student Weizmann Institute of Science (научный руководитель Prof. Vered Rom-Kedar). В 2005 году из ННГУ перевёлся на механико-математический факультет МГУ им. М.В.Ломоносова и переехал в Москву. Окончил МГУ в 2008 году по кафедре Теории функций и функционального анализа (научный руководитель - профессор О.Г.Смолянов), в этом же году поступил в аспирантуру МГУ (к О.Г.Смолянову) и параллельно начал обучение в РЭШ (где был участником научного семинара А.В.Савватеева). Из РЭШ отчислился по собственному желанию в 2009 году, освоив на программе Магистр экономики 3 первых учебных модуля из 10. Кандидатскую диссертацию по математике защитил в МГУ под руководством О.Г.Смолянова в 2018 году, тема диссертации Формулы Фейнмана для параболических дифференциальных уравнений и исчисление функций Чернова.

Работа

В МГУ с 2010 по 2014 годы занимал должность инженера кафедры ТФФА, основной обязанностью была помощь доценту В.П.Серебрякову в проведении занятий и экзаменов по основному курсу функционального анализа и нескольким спецкурсам на мехмате МГУ. В годы работы в МГУ написал методическое пособие "Некоторые факты и обозначения теории множеств", которое с 2012 года в начале первого семестра выдаётся всем студентам первого курса мехмата МГУ (отделение математики и отделение механики). С 2014 по 2017 годы работал ассистентом кафедры Математического моделирования МГТУ им. Н.Э.Баумана, где преподавал математические дисциплины студентам инженерных специальностей, основал и проводил научный семинар по функциональному анализу. В 2016-2018 годах работал в коммерческих структурах (оценочная компания SRG Appraisal, онлайн-банк Tinkoff) в Москве. В 2018 году по приглашению профессора О.В.Починки переехал в Нижний Новгород занять должность доцента кафедры фундаментальной математики ВШЭ и старшего научного сотрудника Лаборатории динамических систем и приложений ВШЭ. В 2023 году оставил позицию доцента (сохранив при этом позицию с.н.с. с дистанционным режимом работы), переехал в Москву и поступил в докторантуру на мехмат МГУ, научный консультант - профессор, член-корреспондент РАН А.А.Шкаликов.

Организационная работа

• Помог открыть совместную с университетом Пассау (Германия) магистратуру с преподаванием на английском языке по направлению "Математика" в НИУ ВШЭ Нижний Новгород в 2018 году, был её первым академическим руководителем, в 2018-2023 годах был членом приёмной комиссии и одним из преподавателей этой магистратуры.

• Инициатор проведения и председатель оргкомитета международных конференций по операторным полугруппам One-Parameter Semigroups of Operators (OPSO) 2021, 2022, 2023. Член программного комитета конференции OPSO 2024.

• Инициатор составления и соавтор-составитель списка открытых проблем в теории операторных полугрупп (черновая версия текста по состоянию на март 2023 выложена здесь.)

• Инициатор проведения и председатель оргкомитета Смотра дипломных работ математиков России 2019-2023.

Преподавание

2014 Математика и экспериментальная физика для школьников 6-10 классов

2014-2017 Высшая математика для инженеров, бакалавриат 1-2 курс: математический анализ (производные и интегралы вещественных функций одной и многих переменных, ряды, начала теории поля), дискретная математика, обыкновенные дифференциальные уравнения, линейная алгебра, аналитическая геометрия, функциональный анализ, комплексный анализ

2018, 2019 Математические дисциплины для математиков: дискретная математика и основы анализа (бакалавриат 1 курс), действительный и функциональный анализ (бакалавриат 2-3 курс)

2018-2023 Спецкурс для математиков: Introduction to one-parameter semigroups of operators with background from real and functional analysis (магистратура 1 курс, на английском языке)

2014-2023 Научный семинар по операторным полугруппам и их приложениям (участники: студенты математики/физики/инженеры начиная с 2 курса бакалавриата, магистранты, аспиранты, исследователи)

Экспертная работа

• Автор обзоров для Mathematical Reviews

• Рецензент научных статей в тематике полугрупп операторов и их приложений

Награды и премии

• Благодарность ректора Российской экономической школы "за помощь в развитии РЭШ" (2013)

• Включён в группу высокого профессионального потенциала (кадровый резерв) НИУ ВШЭ (2019)

• Лауреат премии “лучший преподаватель”, присуждаемой по итогам голосования студентов, магистерская программа Математика НИУ ВШЭ в Н.Новгороде (2021)

• Почетная грамота Министерства образования и науки Нижегородской области "за достигнутые результаты в развитии научно-образовательного комплекса Нижегородской области" (2023)

• Благодарность НИУ ВШЭ-Нижний Новгород "за проявленную инициативу, которая помогла значительно поднять качество работы филиала" (2023)

Personalia

• А.В.Веденин и др. Поздравляем Ивана Ремизова с 35-летием// Веб-сайт ВШЭ

• Биография к конкурсу ППС - май 2023: Remizov-2023

Интересы вне математики

Практикующий психолог, об этой деятельности можно прочитать на сайте психологов b17. Ведущий телеграм-канала о постепенном изменении жизни к лучшему с помощью психологии: https://t.me/remizov_changes.

1. Sonia Mazzucchi, Valter Moretti, Ivan Remizov, Oleg Smolyanov, “Chernoff approximations of Feller semigroups in Riemannian manifolds”, Mathematische Nachrichten, 296:3 (2023), 1244-1284 , arXiv: https://arxiv.org/abs/2002.06606  
2. О. Е. Галкин, И. Д. Ремизов, “Скорость сходимости черновских аппроксимаций операторных $C_0$-полугрупп”, Матем. заметки, 111:2 (2022), 297–299      ; O. E. Galkin, I. D. Remizov, “Rate of Convergence of Chernoff Approximations of Operator $C_0$-Semigroups”, Math. Notes, 111:2 (2022), 305–307      
3. I.D.Remizov, “Formulas that represent Cauchy problem solution for momentum and position Schrödinger equation”, Potential Analysis, 52 (2020), 339–370 https://link.springer.com/article/10.1007        
4. Ivan D. Remizov, “Solution-giving formula to Cauchy problem for multidimensional parabolic equation with variable coefficients”, Journal of Mathematical Physics, 60:7 (2019), 071505 https://aip.scitation.org/doi/10.1063/1.5038102          
5. I.D.Remizov, “Explicit formula for evolution semigroup for diffusion in Hilbert space”, Infinite Dimensional Analysis, Quantum Probability and Related Topics, 21:4 (2018), 1850025 , 35 pp. https://doi.org/10.1142/S021902571850025X            
6. И. Д. Ремизов, “Фейнмановские и квазифейнмановские формулы для эволюционных уравнений”, Доклады Академии наук (математика), 2017, 476, № 1, 17–21      ; I. D. Remizov, “Feynman and Quasi-Feynman Formulas for Evolution Equations”, Doklady Mathematics, 96:2 (2017), 433–437            
7. Ivan D. Remizov, “Quasi-Feynman formulas – a method of obtaining the evolution operator for the Schrödinger equation”, Journal of Functional Analysis, 270:12 (2016), 4540-4557 , arXiv: 1409.8345          

• Национальный исследовательский университет «Высшая школа экономики» (Нижегородский филиал)
• Государственный университет – Высшая школа экономики (Нижегородский филиал)
• Национальный исследовательский Нижегородский государственный университет им. Н. И. Лобачевского
• Московский государственный университет имени М. В. Ломоносова, механико-математический факультет
• Московский государственный технический университет имени Н. Э. Баумана